Généralités Schémas Pratiques
courantesSauvegarde
et restaurationTechniques
avancéesLes agents de
récupérationEn cas de
problème
Le chiffrement intégré des fichiers ("EFS" = Encrypting File System) est une fonctionnalité du système de fichiers NTFS apparue avec la version 3.0, elle-même née avec Windows 2000.
Pour rappel, les versions de NTFS sont les suivantes :
Version
de NTFSVersion de
WINDOWSDisponibilité
de EFS2.0 Windows NT4 3.0 Windows 2000 3.1 Windows XP HOME Windows XP PRO Windows 2003
Sous Windows XP Édition Familiale (HOME),
EFS n'est pas disponible
EFS permet de chiffrer n'importe quel fichier ou dossier appartenant à
une partition NTFS.
Seul l'utilisateur qui a demandé le chiffrement peut accéder au contenu
de ce fichier ou dossier
(et éventuellement des utilisateurs désignés
expressément).
Le chiffrement intégré des fichiers fait fréquemment appel à des acronymes
(pour la plupart en anglais).
Voici la liste de ceux utilisés dans la présente étude :
Acronyme Signification Traduction/Commentaire AES Advanced Encryption Standard Standard de chiffrement avancé (algorithme à clef symétrique)
Conçu en 2000 par Joan Daemen et Vincent Rijmen ("Rijndael")API Application programming interface Interface de programmation d'application
(collections de fonctions mises à disposition des développeurs)CSP Cryptographic Service Provider Service Windows de chiffrement DES Data Encryption Standard Standard de chiffrement de données (algorithme à clef symétrique)
Conçu en 1977 par IBMDESX Data Encryption Standard XORed Variante du précédent DDF Data Decryption Field Champ de déchiffrement de données DRA Data Recovery Agent Agent de récupération de données DRF Data Recovery Field Champ de récupération de données EFS Encrypting File System Système de chiffrement de fichiers FEK File Encryption Key Clef de chiffrement de fichier FIPS Federal Information Processing Standard Standards émis par le National Institute of Standards and Technology
(NIST) pour les systèmes informatiques de l'administration des USAHMAC Hash-Based Message Authentication Code Mécanisme d'authentification de messages utilisant des fonctions de hachage
(RFC 2104)MD5 Message Digest Algorithm 5
Algorithme de hachage développé par RSA Data Security
Il renvoie une valeur de 128 bits.NTFS New Technology File System Système de fichiers "Nouvelle technologie"
Apparu avec Windows NT 3.1 (1993)RSA Rivest Shamir Adleman Algorithme de chiffrement à clefs asymétriques
Conçu par Rivest, Shamir et AdlemanSHA-1 Secure Hash Algorithm Algorithme de hachage publié par le gouvernement US.
L'un des plus utilisé avec MD5. Il renvoie une valeur de 160 bits.SID Security IDentifier Identificateur numérique (128 bits) de compte utilisateur sous Windows
Comme cela vient d'être précisé précédemment, EFS concerne Windows 2000, Windows XP et Windows 2003. Les captures d'écran présentent dans cette étude ont été réalisées essentiellement sous Windows XP
(quelques-unes l'ont été sous Windows 2000 Professionnel).Cependant, sauf mention expresse, tout ce qui est décrit s'applique indifféremment à Windows 2000, XP ou 2003
Les seules différences concernent :
| Version | DESX | 3DES | AES |
| Windows 2000 |
|
|
|
| Windows XP |
|
|
|
| Windows XP + SP1 (et au delà) |
|
|
|
C'est la même clef qui sert à chiffrer puis à déchiffrer le message
Exemple (très basique!) :
Soit un nombre, par exemple 17,
et un algorithme de chiffrement (très simple) consistant à multiplier ce nombre par le code ASCII de chaque lettre du message
Ainsi "HOMER" va être chiffré en :
1224-1343-1309-1173-1394
Ce message chiffré est envoyé à un correspondant, lequel va utiliser la même clef ("17") pour déchiffrer le message, en divisant chaque paquet de chiffres par 17, puis en déterminant le caractère ayant ce code.
1224 / 17 = 72 (code de "H")
1343 / 17 = 79 (code de "O")
1309 / 17 = 77 (code de "M")
1173 / 17 = 69 (code de "E")
1394 / 17 = 82 (code de "R")
Il existe évidemment des algorithmes beaucoup plus complexes que cette simple multiplication, et qui portent non pas sur chaque caractère pris un par un, mais sur un "paquet" de caractères.
L'algorithme le plus connu dans ce domaine est "DES" (Data Encryption Standard - ANSI Standard X3.92-1981).
DES a été conçu au départ par IBM en 1977. Il utilise des clefs de 56 bits (+ 8 bits de parité).
Les données sont découpées en paquets de 64 bits.
A partir de la clef initiale K on fabrique 16 sous-clefs Ki de 48 bits.
Ensuite, pour chaque bloc "x" de 64 bits du texte initial on calcule une permutation y=P(x), mise sous la forme G0 D0 (32 bits gauche et 32 bits droits)On applique 16 fois de suite la même fonction ainsi définie :
pour i= 1 à 16 :
Gi = Di-1
Di = Gi-1 XOR f(Di-1,Ki)
où "f" est une fonction de confusion (substitutions et permutations)On applique enfin à G16 D16 l'inverse de la permutation initiale.
L'algorithme dérivé 3DES consiste à appliquer 3 fois de suite DES
(avec des clefs différentes à chaque fois, ce qui donne une clef globale de 168 bits)
Le principal problème dans cette méthode est qu'il faut transmettre au
préalable la clef au correspondant.
Son intérêt est la rapidité et simplicité.
Cette méthode est appelée également chiffrement à "clef publique et clef
privée".
On génère une paire de clefs (suivant un algorithme plus ou moins complexe),
l'une servant à chiffrer, l'autre à déchiffrer.
L'une des clefs est gardée secrètement (clef privée), l'autre est diffusée à
tout le monde (clef publique).
Dans le cas d'un message envoyé par une personne à une autre, l'expéditeur
chiffre le message avec la
clef publique du destinataire.
Cette clef est connue de tout le monde.
Le destinataire déchiffre le message avec sa clef privée,
qu'il est seul à détenir.
D'où le nom de "chiffrement asymétrique"
L'algorithme le plus connu de cette génération de clefs s'appelle
RSA, du nom de ses concepteurs : RIVEST,
SHAMIR et ADLEMAN
Principe :
Mise en oeuvre :
m message en clair x message chiffré n 1ère partie clef publique e 2ème partie clef publique d clef privée
Chiffrement : x = m^e mod n Déchiffrement : m = x^d mod n
Si les nombres premiers initiaux p et q ont été choisis suffisamment grands, il est quasiment
impossible, à partir de
n et e, de calculer d (à moins de disposer de moyens de calculs considérables)
Exemple :
p = 7 -> n = p.q
n = 119q= 17 (p-1).(q-1) = 96
on choisit (car il y a plusieurs possibilités) :
e = 5 (premier avec 96) d = 77 (5x77 = 4x96 +1) On en déduit les clefs :
clef publique (119 & 5) clef privée 77 Si on prend la lettre H de l'exemple initial, (code 72), elle va être chiffrée ainsi :
72^5 = 1934917632
72^5 mod 119 = 4
Pour retrouver sa valeur :
4^77 = 2,2835963083295358096932575511192e+46
4^77 mod 119 = 72
C'est évidemment un exemple d'école, car on a pris ici des nombres premiers p et q initiaux très petits (7 et 17)
Donc à partir du couple (119,5), il ne faudrait pas longtemps pour retrouver 77
Par contre, si on prend deux nombres premiers très grands, la décomposition du nombre n sera très longue à opérer,
de même que la détermination de d
Envoi de message chiffré et certifié de A vers B.
![]() La
certification, utilisée en plus du chiffrement, permet de garantir la
provenance du message chiffré.
La
certification, utilisée en plus du chiffrement, permet de garantir la
provenance du message chiffré.
Pour que A et B puissent échanger des informations chiffrées et soient capables de les déchiffrer, il faut et il suffit :
Le système à clefs asymétriques est évidemment beaucoup plus lourd et
plus lent que celui à clefs symétriques.
Le problème du chiffrement
symétrique est la communication de la clef unique.
On résout ce dilemme en utilisant conjointement les deux algorithmes de la façon suivante :
Ce système est très sûr et très fonctionnel :
EFS fait appel à un double mécanisme de chiffrement :
Cette mixité a pour but d'améliorer les performances.
En effet, si on utilisait l'algorithme asymétrique pour chiffrer l'intégralité
des données, le temps nécessaire serait prohibitif avec de gros fichiers.
L'algorithme symétrique est environ mille fois plus rapide, ce qui le rend plus
adapté avec un volume important de données.
Mais comme il est plus vulnérable (même clef servant aux chiffrement et
déchiffrement), on chiffre cette clef avec un algorithme asymétrique.
![]() Il ne faut surtout pas renommer ni déplacer ces
dossiers, car le système serait incapable de retrouver les clefs !
Il ne faut surtout pas renommer ni déplacer ces
dossiers, car le système serait incapable de retrouver les clefs !
Par exemple :
C:\Documents and Settings\BELLAMY\Application Data\Microsoft\SystemCertificates\My\Certificates\8E6C255111E32D0A05365191CD8262FC2AC09FB6
Ce fichier est réutilisé pour les chiffrements ultérieurs.
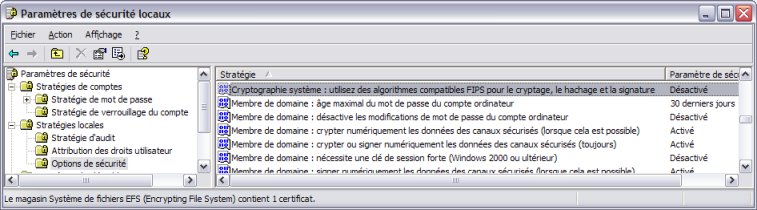
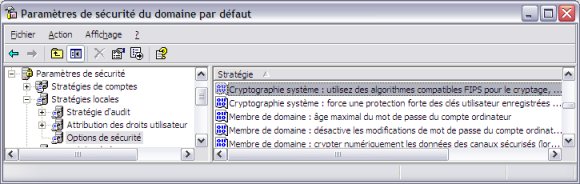
EFS fait appel à la Base de Registres pour déterminer s'il
doit utiliser DESX ou 3DES.
La clef concernée est :
HKLM\SYSTEM\CurrentControlSet\Control\LSA\FipsAlgorithmPolicy
Une valeur égale à 1 indique que 3DES doit être utilisé.
Si ce n'est pas le cas, EFS examine alors la clef :
HKLM\Software\Microsoft\Windows NT\CurrentVersion\EFS\AlgorithmID
Si cette valeur existe, elle peut être égale à :